こんにちは、しおたにです。
これまで、その5でタイヤのゴムズレ対策をし、その6でパラメータ調整を行ったので、以前より安定して曲がれる機体になったと思います。
今回は等速円運動スラロームを試してみます。
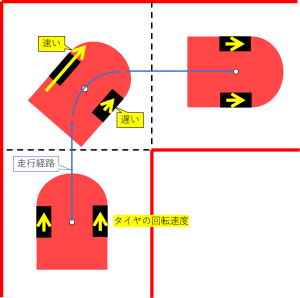
等速円運動スラロームとは速度を変えずに円弧を描きながらカーブを曲がるスラローム走行です。
ざっくり説明すると、外側のタイヤの速度を速く、内側のタイヤの速度を遅く指定することで曲がります。
こちらに詳細にまとめられています。
参考にさせていただきました。
どれくらい速く/遅くすればよいかというと、外側のタイヤと内側のタイヤの旋回中心を一致させるようにすればOKです。
今回はロボット中心の旋回半径を60mm、中心速度が400mm/sになるように曲がることにします。
まず、旋回半径をr、円弧の接線方向の速度をvとし、角速度ωを求めると
式は ω=v/r
ω = 400/60 = 6.6666… ≒ 6.67[rad/s]
となります。
次に各タイヤの速度を求めます。
トレッド幅は67.7mmなので、外側のタイヤの旋回半径は60+67.7/2[mm]、内側は60-67.7/2[mm]となります。
この旋回半径と角速度から外側のタイヤ速度Voutと内側のタイヤ速度Vinを求めると、
式は v = rω
Vout = 93.85*6.67 ≒ 626[mm/s]
Vin = 26.15 * 6.67 ≒ 174[mm/s]
となります。
また、移動距離はロボット中心が描く円弧長なので
2π*r*90[°]/360[°]
から
2*π*60*1/4 ≒ 94[mm]
になります。
以上で等速円運動スラロームに必要な値が求まりました。
ただし、迷路の広さに合わせてスラローム前後に若干の直進を入れてやる必要があります。
諸々の調整後、走らせてみました。
まだ軌跡は美しくないですが、タイムは約8.2秒でした。
ちなみに同じコースを信地旋回で走行した場合、約13.1秒でした。
約4.9秒の短縮です。
スゴイ
信地旋回では内側のタイヤを止める必要があるためどうしてもカーブ進入/脱出速度が制限されてしまいます。
等速円運動スラロームではタイヤを止めなくて良い分カーブの前後を高速にできます。
今回はここまで。ではまた次回。

