車体速度指令値からモータPWMデューティ比を求めるフィードフォワード&フィードバックの計算式を出します。(ただし未検証、修正可能性有)
目的
車体指令速度\( v\)、車体指令角速度\( ω\)、車体指令加速度\( a\)、車体指令角加速度\( α\)から、左右モータのPWMデューティ比を計算する。
PWM
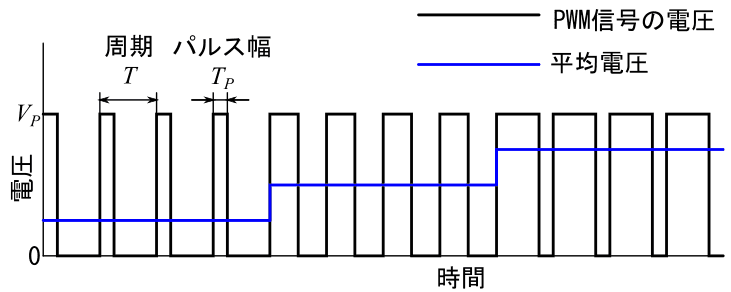
DCモータを制御するときは、マイコンから一定周期のパルスを発生させて、そのパルス幅を変化させることによって平均電圧を制御することができるパルス幅変調(PWM : Pulse Width Modulation)を使ってFETやモータドライバを駆動させる入力信号として使うのが一般的なので、今回はそれにならいます。
ON-FreeやON-BrakeなどFETのHブリッジの開閉に関する話はまた今度。
画像引用:PWMの波形と平均電圧
モータの性質
モータに、指定した角速度で回ってほしい場合は、目標の角速度に逆起電力定数をかけてあげれば、モータに必要な印加電圧を求めることができる。

PID制御
古典制御論の最初で覚える制御法です。これは他の資料に説明を譲ります。Wiki等を見て下さい。
モータPIDフィードバック制御例
モータに取り付けたエンコーダを使って、モータの角速度が目標値になるようモータ印加電圧を求めるよく見かけるPIDフィードバック図です。

目標となるモータの角速度\( ωtaget\)が予めあるとします。モータに印加する平均電圧をデューティ比で調整することで、印加電圧\( e\)としてモータに入力エンコーダから求めた角速度になるようPIDの演算を行い印加電圧\( e\)を求めます。エンコーダは相対角度を計測するセンサなので、微分することで角速度が推定できます。
ただし、自立したマイクロマウスはバッテリ駆動となるので、使っていくうちにバッテリ電圧が変化します。バッテリの電圧が低下するとモータに流れる電圧が小さくなるため、目標値に収束するまでの時間がかかってしまいます。バッテリの電圧に依存しないで同じ操作量としてのモータ印加電圧を出すためには、分圧抵抗などでバッテリの電圧をセンシングすることが再現性を高める上で必須となります。
関数にすると、こんな感じでしょうか?引数にモータ指令角速度\( ωtaget\)、リターン値にモータのデューティ比を出すプログラム関数例です。

とてもシンプルです。ちなみに説明を簡単にするため積分(I成分)の制限は省略してます。
車体のフィードバック制御例
モータのPID制御のおさらいをしたところで、対向独立2輪のリンク情報を元にフィードバック車体制御例1?3を載せます。


車体のフィードバック制御例1
左右のモータを別々のものとして制御する方式

引数に車体指令速度\( v\)、車体指令角速度\( ω\)、リターン値に左右モータのデューティ比を出すプログラム関数例です。

こちらも、左右で2つのモータに増えただけなので、シンプルです。
車体のフィードバック制御例2
車体の速度と角速度をフィードバックさせる制御例

車体のリンク情報をもとに、車体指令速度\( v\)と車体指令角速度\( ω\)から左右モータの速度を出す前に、PIDフィードバックを追加しています。

車体のフィードバック制御例3
ヨー軸回りのジャイロセンサを追加して、フィードバックを入れ替えた場合。

赤で囲ってる部分が例2との違い。

PIDを調整すれば、例3の制御でたいてい完走できると思われます。
車体の力学モデル制御
ここまでは、速度系のみを考えた制御でした。ただ、現実は物理に支配されているため、探索走行などの低速走行のときには摩擦など、最短走行などの高速走行するときには質量やモーメントの加減速を考慮すると制御性が良くなると考えています。
計算式
車体の速度指令値\( v\)と加速度指令値\( ω\)から、左右の必要車輪トルクを算出します。走行環境が綺麗な迷路であれば床摩擦抵抗は0でいいと思います。

次に、車輪周りの慣性モーメントとモータ内部の粘性抵抗、左右の必要車輪トルクを合わせたものを電流に変換します。モータのトルクと電流の関係はトルク定数で比例しています。機械的抵抗(ギア摩擦等)の補償を入れるべきかは迷うところですが、車体が比較的重い場合は要らないかもしれません。

必要な左右モータ電流を割り出したら、インダクタンスの電流変化量を加味するのと、V=IRで実際にモータに印加する平均電圧を計算します。ここはモータモデルとして、モータスペック表やHブリッジ回路のMOSFETに書いている数値が定数となります。もちろん誤差はありますけど。そして、逆起電力分の電圧を追加します。

最後に、デューティ比を求めるために計測した電源電圧で割ってあげます。電源の供給能力が足りない場合、電圧降下が発生したりしますが、ここで計測しておけば補償されるのだと思います。もちろん、モータ印加電圧は昇圧しない限り電源電圧以上に供給できないので、デューティ比に収まるよう設計が必要となります。

車体の動力学制御例
計算式を図にするとこんな感じでしょうか。エンコーダで計測した角速度データが、電流制御器やモータモデルに必要になっていることがわかります。ここでモータへの入力値が角速度ではなくトルクになっているのが大きな違いです。

車体の動力学フィードバック制御例
例3のフィードバックループを採用した図が以下になります。左右モータのエンコーダで車体速度を推定、ジャイロセンサで車体角速度を計測して、各モータへの目標トルクに加味されます。

関数にするとこんな感じ。フィードバック値のPIDVerrorとPIDωerrorは、質量や慣性モーメントを掛け合わせた値として追加します。

はたして、これで綺麗に走行制御できるのでしょうか?
この駆動モデルを実現するための必要部品の選定&回路設計に入ります。
参考文献&引用
【制御工学#1】-カスケード構成のメリット~”位置制御器のみ”と”位置制御器+速度制御”はどちらが良いのか~
【制御工学#2】位置制御器でモータ制御 vs 位置制御+電流制御器でモータ制御してみた。~なんでマイナーループの電流制御器を加えるとよいの?~