d-satoです。初日から在宅勤務のため、自宅でマイクロマウス研修に取り組んでいます。記事一覧はこちらです。
前回は番外編ということでVSCodeを使ってより便利にコードを書いていくため、マイコンに書き込むための設定を紹介しました。
今回はロボットを実際に迷路内で走行させてみます。ただし、Part7ではとりあえず四角形を描くようなコースを走れていましたが、実際に迷路を走行するとなると少し改造が必要です。そこでまず具体的にどのような変更を加えたのかを紹介し、そして変更を加えた結果どのような走行ができるようになったのかを紹介します。
なめらかに迷路を走行してゴールを目指すのに必要なこと
実際にスラローム走行でゴールを目指すには現在地を正しく取得することが重要です。
例えば、現在地から前に1マス、右に2マス進む場合について考えます。
超信地旋回+直進走行での走行の場合は地図内の座標の取得は比較的簡単でした。
以下の図の左のように前に1マス進み、時計回りに90度旋回し、旋回後前に2マス進めば目標位置までたどり着けました。
しかし、スラローム走行の場合は少し異なります。前回、ロボットの中心が半径9cm(迷路の1区画は18cm)の四分円を描くようなコースを走行するようにスラローム走行を実装したので、以下の図の右のように前に0.5マス進み、四分円を描きながら右に90度分曲がり、曲がったあと1.5マス進んで目標位置までたどり着きます。
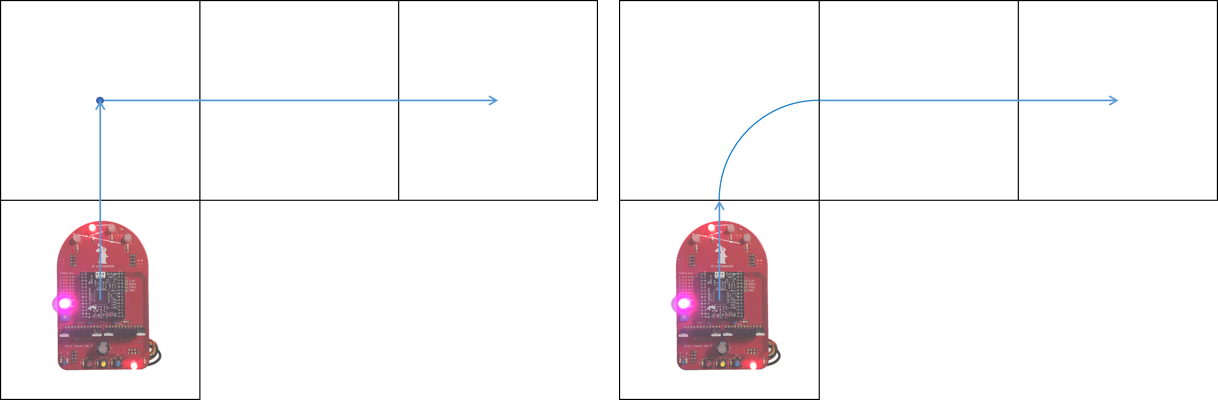
スラローム走行でゴールを目指すための実装
先ほど書いたように、進み方が変わるので迷路内での自己位置の計算方法が少し変わりました。
そこでfast_run()関数を改造したfast_slalom_run()関数を作成しました。

fast_run()関数では直線距離をstraight_countの値に加算して旋回動作がなければ直進するようにしています。fast_slalom_run()でも同様に実装します。
まず、曲がるための動作についてですが、こちらは前回、slalom_rotate()という関数を作成してなめらかに角を曲がれるようにしていたので、その関数を利用しています。
slalom_rotate()関数では実際にはなめらかに曲がっていますが、0.5区画分進む+超信地旋回90度+0.5区画分進むが実装されていると見なして、straight_countに加算する値は調整しています。
fast_slalom_run()関数の処理の該当箇所を一部抜粋します。
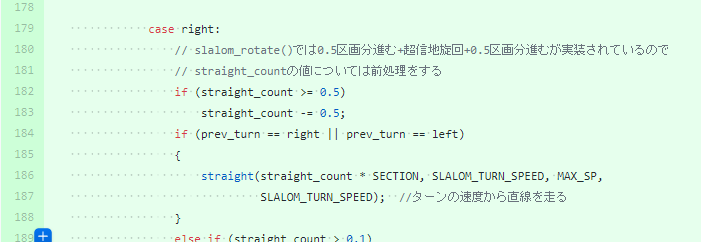
迷路内走行
新しく実装したfast_slalom_run()関数を使って迷路走行をしてみました。
直進+超信地旋回でゴールを目指す従来の走行ではおよそ9秒でスタートからゴールに到達しています。
それに対し、スラローム走行した場合はおよそ5秒でスタートからゴールに到達しています。
大分早くスタートからゴールまでたどり着けるようになりました。
今回実装したスラローム走行で問題なく16×16の迷路を走行させられそうか確認しておきたいので、次回はこれ以外の形状の迷路について走行させます。

