こんにちは。新人のYoです。
前回は出場した2つの大会の結果についてでした。
今回は前回に少しだけ出てきたスラローム走行の実装について書いていこうと思います。
スラローム走行とは
「スラローム走行とは」と検索すると「バイクを左右に傾けながら等間隔に設置された障害物を
交互にかわし、進路転換を行うこと、蛇行運転すること」という検索結果が出てきますが、
マイクロマウスにおけるスラローム走行とは「機体を停止させず滑らかに旋回すること」です。
要するに、一度停止してしまう超信地旋回を使用せず自動車のように旋回させることです。
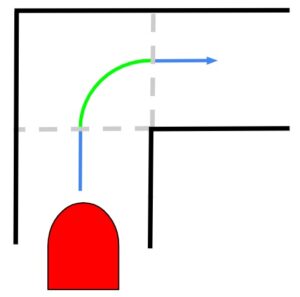
旋回時の軌道はおおよそこのような感じです。
スラローム走行実装手順
スラローム走行には超信地旋回を応用した信地旋回という方法がありますが、
駆動していたモータを急停止させ旋回が終わったら元の速度に戻すといった性質上
脱調やスリップを引き起こす可能性が高く走行の安定性が落ちてしまいます。
台形加減速を利用することで安定した走行が望めるということなので、
今回は台形加減速を利用したスラローム走行を実装します。
また、実装するにあたりクロソイド曲線なるものが重要になってくると教えていただきました。
前々回の探索アルゴリズム実装時と同様にこちらも何度か段階を踏みながら実装していきます。
? クロソイド曲線について理解する
↓
? 計算し理論値を導き出す
↓
? 計算結果を参照しながらスラローム走行を実装する
↓
? 左右それぞれの旋回を調整する
? クロソイド曲線について理解する
クロソイド曲線とは「曲率を一定割合で変化させていった場合に描かれる軌跡」だそうです。
自動車のハンドル操作においては、直進 → カーブ → 直進と運転する場合はハンドルを
一気に切らなければならずかなりの負担がかかります。
しかし、クロソイド部が入ると直進 → クロソイド区間 → カーブ → クロソイド区間 → 直進
となるのでスムーズなハンドル操作が可能になります。
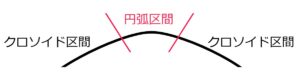
イメージとしてはこんな感じです。詳細はこちらに書かれています。
このクロソイド曲線は身近なものだと高速道路で利用されているそうで、これがあることにより
安全に自動車を走らせることができるとのことです。
何気ない日常の中にもマイクロマウスに応用できる科学があることに驚きです。
? 計算し理論値を導き出す
次に、スラローム走行に必要な値を計算していきます。
直進速度をv = 350 [mm/s]、最小回転半径をr = 50[mm]、最大角速度をω[rad/s]とすると、
v = rω の式から ω = v / r となり ω = 350 / 50 で ω = 7 [rad/s]となります。
続いて旋回の目標角度は90°なので π/ 2 [rad]、角加速度は一旦 α = 40[rad/s?]と置きます。
上記の値からクロソイド区間の時間 t1 と円弧区間の時間 t2 を求めます。
t1 = ω/α
t2 = (π/ 2 – ω?/α ) /ω
これらを計算すると、
t1 = 0.175[s] 単位換算すると t1 = 175[ms]
t2 = 0.049399…[s] 四捨五入して単位換算すると t2 = 49[ms]
これで理論値が算出できました。
? 計算結果を参照しながらスラローム走行を実装する
続いて、先程の計算結果を使用してスラローム走行を実装していきます。
void clothoid_turn_R()
{
straight(10.0, SEARCH_SPEED, SEARCH_SPEED, SEARCH_SPEED); // 直進区間
g_accel = 0;
g_omega_accel = 0;
g_min_speed = 0;
g_max_speed = 1000;
g_con_wall.enable = false;
controlInterruptStart();
g_motor_move = 1;
g_omega_accel = -(40.0)/1000.0;
g_speed = SEARCH_SPEED;
delay(175); // クロソイド区間
g_omega_accel = 0;
g_omega = -7.0;
delay(49); // 円弧区間
g_omega_accel = (40.0)/1000.0;
g_speed = SEARCH_SPEED;
delay(175); // クロソイド区間
clearStepR();
clearStepL();
g_omega_accel = 0;
g_omega = 0;
straight(10.0, SEARCH_SPEED, SEARCH_SPEED, SEARCH_SPEED); // 直進区間
}
これが右旋回専用の関数になります。
ハイライト部分に先程算出した理論値を使用しています。
超信地旋回時と同様に旋回動作の前後に直進区間を追加して調整しています。
クロソイド区間と円弧区間は時間ベースで制御しています。
時間ベースでの制御だと計算結果の最大角速度が 7[rad/s] なので 0.4°ずつしか
調整できませんが、直進時の壁補正も加味してこの精度なら問題ないと判断したので
実装のしやすさと直感的な調整のしやすさからこのようにしています。
void clothoid_turn_L()
{
straight(10.0, SEARCH_SPEED, SEARCH_SPEED, SEARCH_SPEED); // 直進区間
g_accel = 0;
g_omega_accel = 0;
g_min_speed = 0;
g_max_speed = 1000;
g_con_wall.enable = false;
controlInterruptStart();
g_motor_move = 1;
g_omega_accel = (40.0)/1000.0;
g_speed = SEARCH_SPEED;
delay(175); // クロソイド区間
g_omega_accel = 0;
delay(49); // 円弧区間
g_omega_accel = -(40.0)/1000.0;
g_speed = SEARCH_SPEED;
delay(175); // クロソイド区間
clearStepR();
clearStepL();
g_omega_accel = 0;
g_omega = 0;
straight(10.0, SEARCH_SPEED, SEARCH_SPEED, SEARCH_SPEED); // 直進区間
}
左旋回ではハイライト部分のプラスマイナスが逆転します。
? 左右それぞれの旋回を調整する
このプログラムの場合は主に2つの直進区間の値を調整していきます。
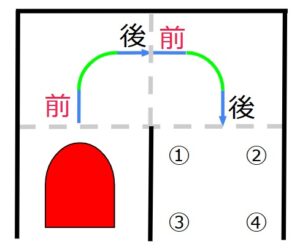
右旋回の調整を行う場合に調整する直進区間は上図のようになります。
旋回動作前の直進区間を増加させた場合、機体の旋回終了位置は?の辺りになります。
逆に、旋回動作前の直進区間を減少させた場合の旋回終了位置は?の辺りなります。
続いて、旋回動作後の直進区間を増加させた場合の旋回終了位置は?の辺りになります。
旋回動作後の直進区間を減少させた場合の旋回終了位置は?の辺りになります。
角度が大きくズレるといった時には円弧区間の値を調整します。
左右の値を分けていることにより必要な調整箇所が増えるというデメリットはありますが、
細かい調整によって左右同値のパラメータより安定した走行が望めるというメリットがあります。
次回予告
次回は東日本地区大会後に実装した「前壁を用いた機体位置補正」について
書いていこうと思います。

