こんにちはinukaiです!
“Cで実装する「実践ロボット制御」“の連載第2回目です!
本日から実際にコードを書いて学んでいきましょう。
まずは、CRANE-X7を2自由度ロボットとして扱うにあたって前提から解説していきます。
CRANE-X7の軸数を減らして取り扱う方法
CRANE-X7の軸数
CRANE-X7はその名の通り、7軸+1軸(エンドエフェクタ)のロボットです。模式図で表すと下記の図のような軸構成になっています。各リンクの長さや可動範囲などのリンク情報のまとめはこちらです。
CRANE-X7を2・3自由度のロボットとして扱う
本連載では初学者でもわかりやすいように、CRANE-X7を2・3自由度のロボットとして扱っていきます。3自由度のロボットとして取り扱う場合は、下記の図のように、アームの根元から数えて3軸目および5?7軸目を固定、2自由度ロボットとして扱う場合は1軸目も固定して取り扱います。手先位置は後々自由度を拡張した際にも計算しやすいよう、エンドエフェクタの先端ではなく手首の3軸(5〜7軸目)が直交した点とします。
本連載で2・3自由度のロボットとして扱う場合のリンク情報はこちらに記載いたしました。

平面2自由度ロボットの運動学
それでは、CRANE-X7を平面2自由度ロボットと見立てて、運動学について考えていきます。
平面2自由度ロボットの順運動学
順運動学問題とは、ロボットアームの関節角度から手先位置を計算する問題です。
「実践ロボット制御」(以降、教科書)の内容を復習していきましょう。
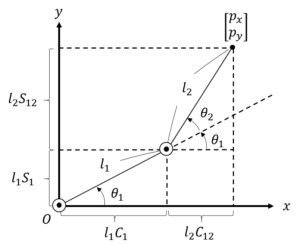
下の図のように、水平方向に\( X \)軸、垂直方向に\( Y \)軸をとり、CRANE-X7の2軸目の角度を\( \theta_1 \)、4軸目の角度を\( \theta_2 \)、手先位置を\( \begin{bmatrix}
p_{x} \\
p_{y}
\end{bmatrix} \)として計算してみます。
もう少し、関節角度と手先位置の関係を図式的に見てみましょう。
図中、教科書と同様に\( S_1 = \sin \theta_1 \)、\( C_1 = \cos \theta_1 \)、\( S_{12} = \sin (\theta_1 + \theta_2) \)、\( C_{12} = \cos (\theta_1 + \theta_2) \)と置き換えて表記しています。ここから、
\begin{align}
\begin{bmatrix}
p_{x} \\
p_{y}
\end{bmatrix}
=
\begin{bmatrix}
l_{1}C_{1} + l_{2}C_{12}\\
l_{1}S_{1} + l_{2}S_{12}
\end{bmatrix}
\end{align}
と教科書の式(1.1)と同様に求めることができます。
平面2自由度ロボットの逆運動学
先ほどの式を、手先位置から関節角度を求める式に変形して逆運動学問題を解いていきます。
まず、\( \theta_2 \)について求めてみましょう。たとえば、\( \theta_2 \)の解き方は二通りあげられます。
- 式変形で求める方法。(こちらは教科書 p.5に詳しい式変形があります!)
- 幾何学的関係から余弦定理を用いて\( C_2 \)を求める方法。
せっかくなので教科書とは別の、2.の方法を使って今回は求めたいと思います。まず、長さ\( l_1 \)、\( l_2 \)のリンクと、原点と手先位置を結んだ3つの辺からなる三角形を考ます。これを図示すると下図のようになります。
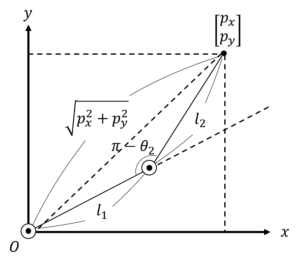
この形を見たら余弦定理で\( C_2 \)が求められそうですね!
余弦定理から、
\begin{align}
p_{x}^2 + p_{y}^2 = l_1^2 + l_2^2 – 2 l_1 l_2 \cos( \pi – \theta_2 )
\end{align}
\begin{align}
p_{x}^2 + p_{y}^2 = l_1^2 + l_2^2 + 2 l_1 l_2 C_2
\end{align}
ここから、
\begin{align}
C_2 = \frac{p_x^2 + p_y^2 – l_1^2 – l_2^2}{2l_1 l_2}
\end{align}
と教科書の式(1.3)と同様に求めることができます。この式が解を持つ条件は、\( -1 \leq C_2? \leq 1 \) より、
\begin{align}
(l_1 – l_2 )^2 \leq p_x^2 +p_y^2 \leq (l_1 + l_2)^2
\end{align}
となります。(教科書の式(1.5)より引用)
式の導出および、式の持つ意味について、詳しくは教科書をご参照ください。
\( \theta_2 \)の解については、\( \cos \theta_2 = \cos ( -\theta_2 ) \)より正と負の2通りあります。図示すると下記のようになります。
ただし、実際にはCRANE-X7の4軸目の可動範囲はリンク情報より-2.74?0 rad(-157°?0°)であることを考慮すると、今回は\( \theta_2 \)が負の解を使用することになります。
あとは\( \theta_1 \)について解くだけです。本記事では導出は省略して結果だけ記載いたします。詳解は教科書をご参照ください。
\begin{align}
\theta_1 = \mathrm{atan2} ( -l_2 S_2 p_x + (l_1 + l_2 C_2) p_y , (l_1 + l_2 C_2) p_x + l_2 S_2 p_y )
\end{align}
(教科書の式(1.9)より引用)
これで、順運動学問題および逆運動学問題が解けましたので、プログラミングしていきましょう。
順運動学および逆運動学のプログラムを作成する
それでは先週のセットアップの続きから、プログラムを作成していきましょう!
本連載では、初学者でも理解しやすいように、プログラムは抽象化などはせず、いわゆるベタ書きで式をそのまま実装していきます。
ただし、今回はプログラム実装の初回ということで、本連載のgithubリポジトリの”common”に用意した今後の連載で共通して用いるファイルの説明も兼ねていますので、少し手順が多いですが、頑張って作っていきましょう。
下準備
まず、robotics_from_scratch/内に”ch02″というディレクトリとその中に”build”ディレクトリを作ります。そしたら、先週の”ch01/build”内のMakefileを先程作ったディレクトリにコピーします。ターミナルでの一連の作業例は下記です。
$ cd ~/robotics_from_scratch $ mkdir -p ch02/build $ cp ch01/build/Makefile ch02/build/Makefile
これでMakefileを使いまわして、ビルドができるようになります。
新規に実施する方は、先週のセットアップに従って環境構築でクローンした状態で「ch02」が存在していると思います。”ch02″の中身を一度削除して、本記事に従って一緒に作成していきましょう!
オリジナルの運動学用のライブラリの作成
これから「実践ロボット制御」の基礎アルゴリズムを実装していく、「自分用のCRANE-X7の運動学・動力学ライブラリ」を作っていきます。
まず、”ch02″内に”myCX7_KDL_library.h”、”myCX7_KDL_library.c”というファイルを作成します。
$ cd ~/robotics_from_scratch/ch02 $ touch myCX7_KDL_library.h myCX7_KDL_library.c
自作ライブラリのヘッダーファイル作成
それでは、自作ライブラリのヘッダファイル”myCX7_KDL_library.h”に、下記を記述します。
#ifndef MYCX7_KDL_LIB_H #define MYCX7_KDL_LIB_H #include "../common/matrix.h" void initParam(void); //// Functions related to kinematics //// int forwardKinematics2Dof(VECTOR_3D *, double *); int inverseKinematics2Dof(VECTOR_3D, double *); #endif
こちらのコードについて説明していきます。
1,2,11行目はインクルードガードです。
4行目は、行列やベクトルを扱うためのmatrixライブラリを読み込んでいます。matrixライブラリは本連載に必要な行列やベクトルの最小限の計算用ライブラリを準備しておいたもので、”common/”フォルダ内にあります。
これを読み込むことで、例えば座標やベクトルを扱うための構造体VECTOR_3D型や行列を扱うための構造体MATRIX_3D型などが使用できるようになります。使い方は実際に使用しながら説明していきますが、VECTOR_3D型およびMATRIX_3D型は”matrix.h”内で下記のように定義されています。
typedef struct
{
double x;
double y;
double z;
} VECTOR_3D;
typedef struct
{
double a[3][3];
} MATRIX_3D;
6行目ですが、これは自分用のCRANE-X7の運動学・動力学ライブラリで扱うアームの物理パラメータを初期化する関数の定義です。詳細はcファイルを作成しながら説明していきますので、とりあえず記述しておきましょう。
8,9行目が、今回のメインの順運動学および逆運動学を計算する関数の定義です。詳細はcファイルを作成しながら説明していきますので、とりあえず記述しておきましょう。
自作ライブラリのソースファイル作成
次に、実際にmyCX7_KDL_library.cを編集して、関数の中身を作っていきます。
#include <stdio.h>
#include <math.h>
#include "../common/arm_parameter.h"
#include "myCX7_KDL_library.h"
static LINK_PARAM link_parameter_3dof[LINK_NUM_3DOF] = {0};
static JOINT_RANGE joint_range[JOINT_NUM] = {0};
void initParam()
{
getLinkParam3Dof(link_parameter_3dof);
getJointRange(joint_range);
}
int forwardKinematics2Dof(VECTOR_3D *p, double *theta)
{
double L1 = link_parameter_3dof[1].length;
double L2 = link_parameter_3dof[2].length;
double C1 = cos(theta[1]);
double C12 = cos(theta[1] + theta[3]);
double S1 = sin(theta[1]);
double S12 = sin(theta[1] + theta[3]);
p->x = L1 * C1 + L2 * C12;
p->y = L1 * S1 + L2 * S12;
return 0;
}
int inverseKinematics2Dof(VECTOR_3D p, double *theta)
{
double L1 = link_parameter_3dof[1].length;
double L2 = link_parameter_3dof[2].length;
double S2, C2;
//手先位置の値が可動範囲の外であればエラー値を返す
if (((pow(L1 - L2, 2)) > (p.x * p.x + p.y * p.y)) || ((p.x * p.x + p.y * p.y) > (pow(L1 + L2, 2))))
{
printf("Target position is out of range.\n");
return 1;
}
//2軸目theta[1]と4軸目theta[3]以外は0 radで固定
for (int i = 0; i < JOINT_NUM; i++)
{
theta[i] = 0;
}
//θ2の角度
C2 = (p.x * p.x + p.y * p.y - L1 * L1 - L2 * L2) / (2 * L1 * L2);
theta[3] = -acos(C2); //acosの戻り値[0:π]、CRANE-X7においてθ2の可動はマイナス方向のみ
//θ1の角度
S2 = sin(theta[3]);
theta[1] = atan2((-L2 * S2 * p.x + (L1 + L2 * C2) * p.y), ((L1 + L2 * C2) * p.x + L2 * S2 * p.y));
//得られた関節角度が可動範囲外であればエラーを返す
for (int i = 0; i < JOINT_NUM; i++)
{
if (((joint_range[i].min) > (theta[i])) || ((theta[i]) > (joint_range[i].max)))
{
printf("Theta[ %d] is out of range.\n", i);
return 1;
}
}
return 0;
}
こちらのコードについて説明していきます。
1行目はおなじみの標準入出力ライブラリです。
2行目はsinやcosを計算するために用いるmathライブラリを読み込んでいます。
3行目は、本連載用のgithubリポジトリの”commom”ディレクトリに用意した、CRANE-X7の物理パラメータを読み込むためのarm_parameterライブラリを使用できるようにします。こちらは本連載用にあらかじめ準備しました。
4行目は、本自作ライブラリのヘッダーファイルを読み込んでいます。
パラメータの初期化関数
6、7行目は各リンクの物理パラメータと各軸の可動範囲を本自作ライブラリ内で用いるための変数定義です。
ここで、arm_parameterライブラリに触れておきます。
6行目のLINK_PARAM型は、”/common/arm_parameter.h”内に下記のように定義されています。
メンバ変数はそれぞれ、massはリンクの重量、lengthはリンク長、comはローカル座標系の重心位置、inertia_tensorはローカル座標系の慣性テンソルを格納できるようになっています。
(今回からしばらくの間は、運動学といった幾何学計算になるため、リンク長のみをもちいますが、連載が進み動力学までいくと、重量や重心位置、慣性モーメントといったパラメータを使用します。)
typedef struct
{
double mass;
double length; // link length
VECTOR_3D com; // centor of mass position (local coordinate)
MATRIX_3D inertia_tensor; // tensor of inertia (coordinates from the center of mass)
} LINK_PARAM;
また、LINK_PARAM型のlink_parameter_3dof配列の数LINK_NUM_3DOFは、CRANE-X7を3自由度のロボットとして扱う際のリンクの数で、”/common/arm_parameter.h”内に下記の様に定義されています。
#define LINK_NUM_3DOF (3)
7行目のJOINT_RANGE型は、”/common/arm_parameter.h”内に下記のように定義されています。
メンバ変数はそれぞれ、minは可動範囲の下限、maxは可動範囲の上限を格納できるようになっています。
typedef struct
{
double min;
double max;
} JOINT_RANGE;
また、JOINT_RANGE型のjoint_range配列の数JOINT_NUMは、CRANE-X7の軸数で、”/common/arm_parameter.h”内に下記の様に定義されています。
#define JOINT_NUM (8)
次に、9〜13行目は、先程の物理パラメータおよび各軸の可動範囲を自作ライブラリ内で用いることができるように、”/common/arm_parameter.c”から読み出す関数です。これは、ライブラリを最初に用いる際に必ず実行する関数となります。これでリンク情報に記載された物理パラメータや可動範囲の情報をLINK_PARAM型やJOINT_RANGE型の構造体変数として読み出せるようになります。物理パラメータや可動範囲の使い方は、実際に以降の例を見ながら解説していきます。(関数の説明は割愛しますが、簡単な関数なので”/common/arm_parameter.c”を参照していただければと思います。)
順運動学を計算する関数
それでは、15〜24行目の順運動学を計算する関数を見ていきます。
関数は下記のような定義とします。
- int forwardKinematics2Dof(VECTOR_3D p, double *theta)
- 引数:手先位置の格納先のVECTOR_3D型のポインタ *p (x,yのみ使用)、および関節角度の配列のポインタ *theta
- 戻り値:予約
引数の*pは、手先位置の計算結果を格納する(VECTOR 3D型の構造体変数のポインタです。 theta は各関節角度の配列ポインタです。theta には、CRANE-X7 の第 1 関節から第 7 関節までとグリッパーの角度が順番に格納された配列変数のポインタが与えられるとします。
戻り値については、エラー処理などに使用するため予約 としていますので、必要に応じて使用してください。逆運動学問題を 解く関数を実装する場合などでは、エラー処理を実装するために戻り値を使用し ます。これは計算結果が可動範囲外の値となった場合に、その結果をロボットに指令すると予想しない動きをする可能性があるためです。一方、今回 のような順運動学問題を解くうえでは、その計算結果は直接ロボットに与える値ではないため、エラー処理を実装しません。
次に、各行の説明です。
17、18行目では、平面2自由度ロボットのリンク長L1、L2を格納する変数を定義し、9〜13行目で読み込んだリンク長(link_parameter_3dof構造体のメンバ変数lengthに格納されている)で値を初期化しています。
20〜23行目は、sin や cos の値を格納する変数を定義して、値を計算しています。平面 2 自由度ロボットの θ1 は CRANE-X7 の2軸目(対応する変数:theta[1])、θ2 は CRANE-X7 の4軸目 (対応する変数:theta[3])が対応しています。
25、26行目が、実際に順運動学を解く式で、たったの2行で済みます。これは教科書の式(1.1)そのものですね。変数名と数式中の記号を見やすいように置き換えていますが、ここは好みの問題なので変数の値の置き換えをしなくても問題ありません。ただ、これから数式が複雑になってきても、数式とプログラムの対応が確認しやすいよう本連載ではこのように変数を数式中の記号に近いかたちで表現することとします。
逆運動学を計算する関数
次に、31〜66行目の逆運動学を計算する関数を見ていきます。
関数は下記のような定義とします。
- int inverseKinematics2Dof(VECTOR_3D p, double *theta)
- 引数:手先位置の構造体変数 p (x,y のみ使用)、および関節角度を格納する配列変数のポインタ *theta
- 戻り値:可動範囲内であれば正常値 0、可動範囲外であればエラー値 1 を返す
手先の座標は、VECTOR 3D 型の構造体の引数として関数に渡します。各関節角度の計算結果は、配列変数のポインタを用いて引き渡しをします。この関数は、 CRANE-X7 が平面 2 自由度ロボットとして動作するように、手先の x, y 座標である p.x,、p.y から、CRANE-X7 の2軸目の角度 theta[1](平面 2 自由 度ロボットの θ1)と4軸目の角度 theta[3](平面 2 自由度ロボットの θ2)を計算します。その他の関節角度は 0 rad とします。
戻り値は、指定した座標、あるいは計算された関節角度が可動範囲内かどうかを判定した結果を返します。逆運動学問題を解く関数を実装する場合などでは、計算結果が可動範囲外の値となった場合にその結果をロボットに指令すると、ロボッ トが予想しない動きなどをする可能性があります。そのため、エラー処理を実装する必要があります。例えば、この関数をメイン関数から呼び出すときに戻り値でエラーを検出したらロボットを止める、プログラムを停止する、手先位置を変更して再度計算するなどの処理をすればよいです。
次に、各行の説明です。
33、34 行目は、θ2を求めるために使用するS2、C2の変数定義です。
順運動学の時と同様に、リンク長の変数の定義と、リンク長を変数に代入しています。
39〜43行目は、教科書の式(1.5)より、逆運動学を解く関数に与えられた手先位置が、逆運動学の解が存在する範囲であるか(可動範囲に収まっているか)判別しています。解が存在しない範囲である場合、エラーメッセージを表示、エラー値を返して関数を終了します。
45〜49行目は、CRANE-X7の各関節の値を0で初期化しています。
52〜56行目が、逆運動学の計算になります。
52、53行目は教科書の式(1.3)を用いてθ2を計算し、CRANE-X7の4軸目の角度を格納する配列要素theta[3]に代入しています。また、可動範囲から値が負の解を選んでいます。
55、56行目でθ1の解を計算して、CRANE-X7の2軸目の角度を格納する配列要素theta[1]に代入しています。
59〜67行目は、解いた逆運動学の解が、CRANE-X7の各関節の可動範囲の中にあるか確認しています。各関節の可動範囲は9〜13行目で初期化したjoint_range構造体に格納されているので、例えば、可動範囲の最小値はjoint_range[i].min(最大値はjoint_range[i].max)と行った形で使用することができます。可動範囲外であれば、エラーメッセージを表示、エラー値を返して関数を終了します。
67行目、可動範囲内の関節角度の値として逆運動学の解が求まれば、戻り値に0を返して関数を終了します。
以上で、平面2自由度の順運動学および逆運動学を求める関数を実装できたので、確認していきましょう。
動かす前に数値で確認をする
それでは、「ch02」内に「main.c」というファイルを作成して、下記の内容を書いてみましょう。
こちらは、最低限関数の用法などを確認するコードに留めています。
#include <stdio.h>
#include "../common/arm_parameter.h"
#include "myCX7_KDL_library.h"
int main()
{
double theta1[JOINT_NUM] = {0.0, 1.789936, 0.0, -2.403867, 0.0, 0.0, 0.0, 0.0};
double theta2[JOINT_NUM] = {0};
VECTOR_3D pos1 = {0};
VECTOR_3D pos2 = {0.25, 0.15, 0};
initParam();
forwardKinematics2Dof(&pos1, theta1);
inverseKinematics2Dof(pos2, theta2);
printf("Forward kinematics result [θ1 θ2]:[%lf %lf] -> [x y]:[%lf %lf]\n", theta1[1], theta1[3], pos1.x, pos1.y);
printf("Inverse kinematics result [x y]:[%lf %lf] -> [θ1 θ2]:[%lf %lf]\n", pos2.x, pos2.y, theta2[1], theta2[3]);
return 0;
}
こちらについて簡単に説明します。
7行目に順運動学を解く関数に与える関節角度を予め用意した配列変数、8行目に逆運動学の結果の関節角度を格納する配列変数を定義しています。
10行目に順運動学を解いた結果を格納する手先位置を格納する構造体、11行目に逆運動学を解く関数に与える手先位置を予め用意した構造体を定義しています。
位置の単位は[m]、角度の単位は[rad]です。
13行目で、自作ライブラリ”myCX7_KDL_library”で使用するアームの物理パラメータを初期化します。
15、16行目で順運動学と逆運動学をそれぞれ計算します。
18、19行目で計算結果を表示しています。
それでは実行していきましょう。
自作のライブラリをコンパイルの対象にするために、Makefileの66行目に下記のように”myCX7_KDL_library.c \“という行を追加してください。
#---------------------------------------------------------------------
# Files
#---------------------------------------------------------------------
SOURCES = main.c \
$(DIR_COM)/crane_x7_comm.c \
$(DIR_COM)/arm_parameter.c \
$(DIR_COM)/matrix.c \
myCX7_KDL_library.c \
これで、コンパイルと実行が可能になります。
コンパイルおよび実行すると下記のように、順運動学と逆運動学の計算結果が出力されます。
$ cd ~/robotics_from_scratch/ch02/build $ make $ ../bin/crane_x7_test Forward kinematics result [θ1 θ2]:[1.488682 -1.896526] -> [x y]:[0.250000 0.150000] Inverse kinematics result [x y]:[0.250000 0.150000] -> [θ1 θ2]:[1.488682 -1.896526]
実際に数値を確認すると、教科書の式(1.1)、(1.3)および(1.9)を満たしていることが確認できます。上記プログラムでは、順運動学・逆運動学それぞれ1点ずつしか確認していませんが、平面2自由度の問題は2変数の連立方程式であったため、それぞれ最低限2点以上値を確認して関数の実装に問題がないか確認しておきましょう!また、可動範囲外ではエラーが返ってくるかどうかも確認してみましょう。
結果を確認する際には、scanfなどで値を入力したら結果を見れるようにするなど工夫してみてください。
CRANE-X7を動かして確認する
CRANE-X7を動かすために使用する関数
プログラムを説明する前に、CRANE-X7との通信方法について説明しておきます。
“../common/”内のcrane_x7_commにCRANE-X7と通信する関数が用意されています。この関数が実際には先週インストールしたDynamixelSDKを内部で利用して通信を行っています。
今回使用する関数を紹介しておきます。使用例はソースコードを追って説明します。
-
initilizeCranex7(uint8_t *):これは、CRANE-X7の各ジョイントの動作モード(位置・速度・電流モード)を指定して通信を初期化します。
-
setCranex7TorqueEnable(uint8_t *):CRANE-X7の各軸のトルクをONにします。例えば位置制御モードではトルクをONにすると角度に制御がかかり始めます。
-
setCranex7Angle(double *):CRANE-X7の各軸に対して、角度指令値を送信する関数です。
- getCranex7JointState(double *, double *, double *):CRANE-X7の各軸の状態を取得する関数です。引数は順番に現在の角度、速度、トルクの順番です。
- brakeCranex7Joint():CRANE-X7をブレーキ状態にする関数です。エラー時や動作終了時に使用できます。
- closeCranex7Port():通信に使用しているシリアルポートを閉じます。
CRANE-X7を動かすメイン関数
それでは、”ch02″内の”main.c”を”main1.c”などに変更しておいて、新しい「main.c」を作成して下記の内容を書いてみましょう。
コマンド操作の場合の例は下記です。
$ cd ~/robotics_from_scratch/ch02 $ mv main.c main1.c $ touch main.c
#include <stdio.h>
#include <unistd.h>
#include "../common/crane_x7_comm.h";
#include "myCX7_KDL_library.h";
int main()
{
uint8_t operating_mode[JOINT_NUM] = {POSITION_CONTROL_MODE, POSITION_CONTROL_MODE, POSITION_CONTROL_MODE, POSITION_CONTROL_MODE, POSITION_CONTROL_MODE, POSITION_CONTROL_MODE, POSITION_CONTROL_MODE, POSITION_CONTROL_MODE};
VECTOR_3D target_pos = {0}; //目標位置格納用の変数
VECTOR_3D target_pos1 = {0.25, 0.15, 0}; //目標位置1
VECTOR_3D target_pos2 = {0.35, 0.15, 0}; //目標位置2
VECTOR_3D target_pos3 = {0.35, 0.25, 0}; //目標位置3
VECTOR_3D target_pos4 = {0.25, 0.25, 0}; //目標位置4
VECTOR_3D present_pos = {0}; //現在位置格納用の変数
double target_theta[JOINT_NUM] = {0}; //目標角度格納用の変数
double present_theta[JOINT_NUM] = {0}; //現在角度を格納する変数
double present_angvel[JOINT_NUM] = {0}; //現在速度を格納する変数
double present_current[JOINT_NUM] = {0}; //現在トルクを格納する変数
int state = 0; //目標位置を切り替えるための変数
int cnt = 0; //ループのカウント
printf("Press any key to start (or press q to quit)\n");
if (getchar() == ('q'))
return 0;
// 運動学ライブラリの初期化
initParam();
// サーボ関連の設定の初期化
if (initilizeCranex7(operating_mode))
{
return 1;
}
// CRANE-X7のトルクON
setCranex7TorqueEnable(TORQUE_ENABLE);
target_pos = target_pos1;
// main関数のループ
while (cnt < 9)
{ //10回繰り返したらプログラムを終了する
cnt++;
if (inverseKinematics2Dof(target_pos, target_theta))
{
break;
}
setCranex7Angle(target_theta);
sleep(3);
getCranex7JointState(present_theta, present_angvel, present_current);
forwardKinematics2Dof(&present_pos, present_theta);
printf("Target position [x y]:[%lf %lf]\n", target_pos.x, target_pos.y);
printf("Present position [x y]:[%lf %lf]\n", present_pos.x, present_pos.y);
//target_angleを変更
if (state == 0)
{
state = 1;
target_pos = target_pos2;
}
else if (state == 1)
{
state = 2;
target_pos = target_pos3;
}
else if (state == 2)
{
state = 3;
target_pos = target_pos4;
}
else
{
state = 0;
target_pos = target_pos1;
}
} //end main while
brakeCranex7Joint(); //CRANE X7をブレーキにして終了
closeCranex7Port(); //シリアルポートを閉じる
return 0;
}
2行目は、sleep関数を使用できるようにするためにunistdをインクルードします。
3行目は、先程簡単に説明した、”common”内に用意されているCRANE-X7と通信するための関数を使用できるようにしています。
4行目は、先程作成した自作のライブラリを読み込んでいます。
それではメイン関数の説明に入ります。
8行目は、CRANE-X7の動作モードを指定するための配列定義です。initilizeCranex7()関数に与える引数です。今回はモータを位置制御モードで使用するため、配列の中身はすべてPOSITION_CONTROL_MODEとします。(POSITION_CONTROL_MODEの値は”crane_x7_comm.h”内に定義されています。)
9〜22行目は、変数の定義です。これらは使用するタイミングで説明します。
24〜26行目は、プログラムを実行後にいきなりロボットが動き出さないようにキー入力を待ちます。qを入力すると終了し、それ以外の入力でプログラムを開始します。
29行目は、自作のライブラリ用のパラメータの初期化です。
32〜35行目は、CRANE-X7との通信を初期化します。引数に8行目で定義した配列を渡して、動作モードを位置制御にします。
37行目は、CRANE-X7のトルクがONになり、位置制御を開始します。CRANE-X7の関節が脱力した状態から制御がかかった状態になります。
39行目は、手先位置の指令値を初期化します。
42〜80行目が、CRANE-X7が実際に動作するプログラムです。順を追ってみていきます。
このループは9回繰り返されます。繰り返すごとに44行目で、cntをインクリメントします。
46〜49行目で、逆運動学を解いて、手先位置の指令値を関節角度の指令値に変換しています。もし逆運動学が解けない場合はwhile文を抜けてプログラムを終了します。
50行目で、逆運動学を解いた結果の関節角度指令値をCRANE-X7に送ります。
52行目は、CRANE-X7が司令した角度に動くまで待つために3秒間sleepして待ちます。
54行目は、指令した角度に動いたあとに、CRANE-X7の角度や速度、トルクといった値を取得しています。今回は角度の値だけその後に用います。
55行目で、現在角度から順運動学を計算して手先位置を計算します。
55〜56行目で、指令した手先位置と実際の手先位置にどの程度差があるかを画面に出力して確認します。
60〜79行目は、手先位置の指令値をループの繰り返し回数ごとに変化させています。
82行目は、動作が終わったら動作を終了する前にCRANE-X7をブレーキモードにします。これをすることでゆっくりとCRANE-X7が脱力します。
84行目で、CRANE-X7との通信ポートを閉じて終了します。
CRANE-X7を実際に動かして確認する
それでは、コンパイルして実行しましょう。コンパイル方法は先週と同様、”ch02/build/”ディレクトリに移動してmakeコマンドを実行します。
../bin/crane_x7_testで実行できます。動かした動画は下記になります。このように手先位置(手首の3軸が直行している場所)が四角を描くように動けば成功です!
下記に、コンパイルと実行時に必要なコマンドと、実行時にターミナルに表示される例を示します。
実行時に指令した位置と実際の位置がどの程度ずれているかが確認できます。サーボのゲインがデフォルトの値だと1〜2cm程度絶対位置はずれますね(特に重力方向、サーボのゲイン設定は本連載では深く触れませんが、時間があればそのあたりも書きたいですね。)
$ ~/robotics_from_scratch/ch02/build $ make $ sudo chmod 666 /dev/ttyUSB0 $ ../bin/crane_x7_test <省略> Target position [x y]:[0.250000 0.150000] Present position [x y]:[0.247578 0.137528]
おまけ(手首姿勢のヒント)
今回は手首の姿勢について触れませんでしたが、平面2自由度のロボットとして使用する場合でも、CRANE-X7の6軸目の角度を制御すれば手首を利用できます。
例えば、平面2自由度の逆運動学の解に6軸目の角度を下記のような行を追加してあげれば、写真のように手首を常に下に向けるようなことができます。これならピックアンドプレイスなども作れるかと思います。
(手の開閉はtheta[7]に値を入れてあげればできます。)
#define PI (3.141592) <省略> theta[5] = -PI/2 - theta[1] - theta[3];
まとめ
今回は、平面2自由度ロボットの順運動学および逆運動学をCRANE-X7を題材に解いてみました。また実際に動かすプログラムを作成しました。今回のプログラムは本ブログ連載のgithubリポジトリにアップロードされていますので、躓いたらそちらを見てみてください。
それでは次回は垂直3自由度の問題を考えていきます。
ではまた次回!

![Cで実装する「実践ロボット制御」[2] 〜2自由度ロボットの順運動学と逆運動学〜](https://rt-net.jp/humanoid/wp-content/uploads/2020/06/795316b92fc766b0181f6fef074f03fa.png)