新入社員の中村です。前回のMoveIt 2を使用したピックアンドプレイスに続いて、独自の軌道生成アルゴリズムのための逆運動学を実装します。逆運動学は、手先の位置姿勢が与えられたときに、それを実現する各関節角度を求めることを指します。本記事では、CRANE-X7を6自由度のアームに見立てて、与えられた手先の位置姿勢を実現する関節角度を幾何学的かつ解析的に求めます。
問題設定
本記事では、簡単のために、CRANE-X7を6自由度アームに見立てます。3自由度アームの逆運動学については、Cで実装する「実践ロボット制御」[3] 〜3自由度ロボットの順運動学と逆運動学〜を参照してください。以下に6自由度アームに見立てたCRANE-X7を示します。
\(\Sigma_w\)はワールド座標系、\(\Sigma_h\)は手先座標系、\(\Sigma_1,\cdots,\Sigma_6\)は各関節の座標系、\(l_1,,\cdots,l_6\)は各リンクの長さを表します。\(\Sigma_1\)では\(z\)軸、\(\Sigma_4\)と\(\Sigma_6\)では\(x\)軸、その他の座標系では\(y\)軸が回転します。手先の位置\((x,y,z)\)とロール・ピッチ・ヨー角\((\phi,\theta,\psi)\)が与えられたときの各関節の回転角度\(\theta_1,\cdots,\theta_6\)を求めます。
回転行列(ロールピッチヨー)
ロール・ピッチ・ヨーを用いた回転の表現では、\(x\)軸の回転をロール、\(y\)軸の回転をピッチ、\(z\)軸の回転をヨーと呼び、固定された座標系についてロール・ピッチ・ヨーの順番で軸を回転させることで空間での回転を表現します。ロール・ピッチ・ヨーの回転角度を\((\phi,\theta,\psi)\)とすると、各軸での回転を表す行列は、以下のようになります。
\begin{align}
R_x(\phi)&=
\begin{bmatrix}
1&0&0\\
0&\cos\phi&-\sin\phi\\
0&\sin\phi&\cos\phi
\end{bmatrix}\\
R_y(\theta)&=
\begin{bmatrix}
\cos\theta&0&\sin\theta\\
0&1&0\\
-\sin\theta&0&\cos\theta
\end{bmatrix}\\
R_z(\psi)&=
\begin{bmatrix}
\cos\psi&-\sin\psi&0\\
\sin\psi&\cos\psi&0\\
0&0&1
\end{bmatrix}
\end{align}
ロール・ピッチ・ヨーを順に回転させて得られる行列\(R_{rpy}(\phi,\theta,\psi)\)は、次のように求まります。
\begin{equation}
R_{rpy}(\phi,\theta,\psi)\equiv R_z(\psi)R_y(\theta)R_x(\phi)
\end{equation}
行列の積の順番に注意してください。ワールド座標のある点\(p\)に対して回転\(R_{rpy}(\phi,\theta,\psi)\)を作用させると回転された点\(p’\)が得られます。
\begin{equation}
p’=R_{rpy}(\phi,\theta,\psi)p
\end{equation}
また、回転\(R_{rpy}(\phi,\theta,\psi)\)が作用されたローカル座標系から見た\(p\)を\(\bar p\)とすると、次の関係が成り立ちます。
\begin{equation}
p=R_{rpy}(\phi,\theta,\psi)\bar p
\end{equation}
回転\(R_{rpy}(\phi,\theta,\psi)\)は、ローカル座標系の姿勢を表し、ローカル座標系での点をワールド座標系に座標変換します。さらに、ローカル座標系の位置が\((x,y,z)\)で与えられたとき、ローカル座標系の点\(\bar p\)は、ワールド座標で点\(p\)として次のように表されます。
\begin{equation}
p=R_{rpy}(\phi,\theta,\psi)\bar p+\begin{bmatrix}x\\y\\z\end{bmatrix}
\end{equation}
逆運動学の解法
最初に、手先の位置姿勢から、\(\Sigma_5\)の位置\((x_5,y_5,z_5)\)を求めます。手先の位置\((x,y,z)\)とロール・ピッチ・ヨー角\((\phi,\theta,\psi)\)が与えられたとき、\(\Sigma_5\)の位置\((x_5,y_5,z_5)\)は次のように求まります。
\begin{equation}
\begin{bmatrix}x_5\\y_5\\z_5\end{bmatrix}=
R_{rpy}(\phi,\theta,\psi) \begin{bmatrix}l_5+l_6\\0\\0\end{bmatrix}+\begin{bmatrix}x\\y\\z\end{bmatrix}
\end{equation}
\(\Sigma_5\)の位置\((x_5,y_5,z_5)\)が求まると、\(\theta_1\)が求まります。
\begin{equation}
\theta_1=\mathrm{atan2}(y_5,x_5)
\end{equation}
atan2(y,x)は、C/C++の標準ライブラリで提供されている関数で、点\((x,y)\)と原点を通る直線とx軸のなす角を返します。
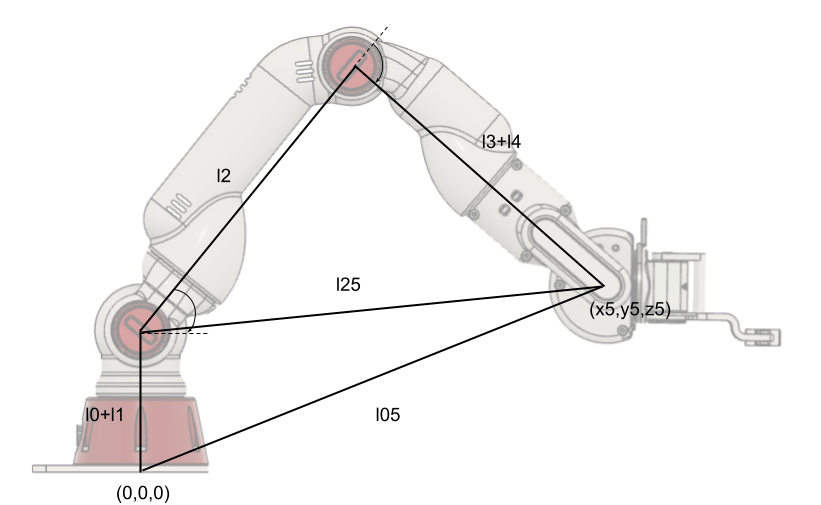
次に、\(\theta_2,\theta_3\)を求めます。以下の図から、幾何学的に求まります。
余弦定理より、\(\theta_2,\theta_3\)は次のように求まります。
\begin{align}
\frac{\pi}{2} – \theta_2 &= \arccos{\frac{(l_0+l_1)^2+l_{25}^2-l_{05}^2}{2(l_0+l_1)l_{25}}}+\arccos{\frac{l_2^2+l_{25}^2-(l_3+l_4)^2}{2l_2l_{25}}}\\
\pi-\theta_3&=\arccos{\frac{l_2^2+(l_3+l_4)^2-l_{25}^2}{2l_2(l_3+l_4)}}\\
l_{05}&=\sqrt{x_5^2+y_5^2+z_5^2}\\
l_{25}&=\sqrt{x_5^2+y_5^2+(z_5-l_0-l_1)^2}
\end{align}
最後に、\(\theta_4,\theta_5,\theta_6\)を求めます。手先の姿勢と各関節の回転との関係は、次のように表されます。
\begin{equation}
R_{rpy}(\phi,\theta,\psi)=R_z(\theta_1)R_y(\theta_2)R_y(\theta_3)R_x(\theta_4)R_y(\theta_5)R_x(\theta_6)
\end{equation}
回転行列\(R\)について、\(R^{-1}(\theta)=R(-\theta)\)だから、次のように変形することができます。
\begin{equation}
R_x(\theta_4)R_y(\theta_5)R_x(\theta_6)=R_y(-\theta_3)R_y(-\theta_2)R_z(-\theta_1)R_{rpy}(\phi,\theta,\psi)
\end{equation}
左辺を計算すると、次のように表されます。
\begin{equation}
R_x(\theta_4)R_y(\theta_5)R_x(\theta_6)=
\begin{bmatrix}
c_5&s_5s_6&s_5c_6\\
s_4s_5&c_4c_6-s_4c_5c_6&-c_4s_6-s_4c_5c_6\\
-c_4s_5&s_4c_6+c_4c_5s_6&-s_4s_6+c_4c_5c_6
\end{bmatrix}
\end{equation}
ここで、\(s_4\)と\(c_4\)は、それぞれ\(\sin\theta_4\)と\(\cos\theta_4\)を表します。右辺について、
\begin{equation}
R_y(-\theta_3)R_y(-\theta_2)R_z(-\theta_1)R_{rpy}(\phi,\theta,\psi)=
\begin{bmatrix}
R_{11}&R_{12}&R_{13}\\
R_{21}&R_{22}&R_{23}\\
R_{31}&R_{32}&R_{33}
\end{bmatrix}
\end{equation}
とおきます。左辺と右辺の行列の対応する要素が等しいことから、\(\theta_4,\theta_5,\theta_6\)は、次のように求まります。
\begin{align}
\theta_4&=\arctan{\frac{R_{21}}{-R_{31}}}\\
\theta_5&=\arctan{\frac{-R_{31}}{c_4R_{11}}}\\
\theta_6&=\arctan{\frac{R_{12}}{R_{13}}}
\end{align}
ただし、\(\theta_4,\theta_5,\theta_6\)は\([-\pi/2,\pi/2]\)に制限されます。
実機での検証
前節で求めた逆運動学の式を実装し、目標の位置姿勢を実現する関節角度を求め、CRANE-X7を制御します。以下の動画では、手先をある位置でヨー角45度の姿勢をとるように制御しています。
動画で示されているように、手先を目標の位置姿勢に制御することができています。
おわりに
本記事では、6自由度アームの逆運動学を計算し、CRANE-X7の手先を目標の位置姿勢に制御しました。これにより、目標の位置姿勢を関節角度空間で表すことができ、関節角度空間内で軌道生成を行うことができるようになります。次回は、重力補償を用いた制御と躍度最小軌道を用いた軌道生成を行います。